1. Einleitung
Induktivitäten werden mit Widerständen ® und Kondensatoren © parallel verbunden. Wichtige passive Komponenten werden manchmal als Spulen bezeichnet. Normalerweise bezieht sich eine Spule auf eine kreisförmige Drahtwicklung und die Spule in einem Stromkreis bezieht sich auf einen Induktor.
Das Symbol eines Induktors wird normalerweise durch „L“ dargestellt. Dieser Schritt ist eine Erinnerung an den russischen Physiker Heinrich Lenz.

Der Grundaufbau eines Induktors besteht darin, die Drähte in eine Spulenform zu wickeln, die elektrische Energie in magnetische Energie umwandeln und im Inneren des Induktors speichern kann. Die akkumulierte magnetische Energie wird durch den Induktivitätswert des Induktors bestimmt, und die Einheit des Induktivitätswerts ist Henry (H).

2. Die Grundstruktur der Induktivität

Der einfachste Induktor ist ein Induktor, der Drähte in eine Spulenform wickelt, mit externen Anschlüssen an beiden Enden des Drahtes. In den letzten Jahren wurde ein großer Teil der Induktoren durch das Wickeln von Drähten um Magnetkerne hergestellt.

Der Induktivitätswert einer Induktivität kann mit der folgenden Formel berechnet werden:

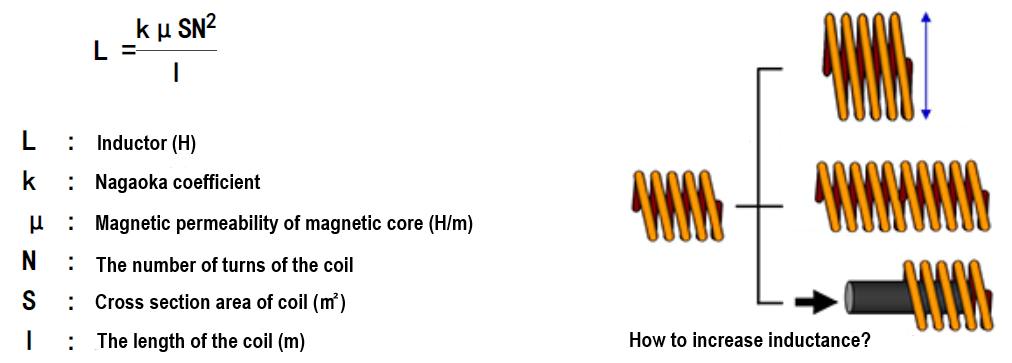
3. Symbol für Induktivität

Typ
Induktor (ohne Magnetkern)
Induktor (Eisenkern)

4. Spannung und Strom der Induktivität
Wie in der Struktur angegeben, werden Induktivitäten durch einfaches Wickeln von Drähten hergestellt, sodass beim Anlegen einer Spannung grundsätzlich ein Strom durch sie fließt. Bei Induktoren handelt es sich jedoch um Komponenten, die elektromagnetische Induktion nutzen und nicht einfach nur Strom durch sie fließen lassen. Dies erklärt die Funktion der Induktivität beim Anlegen von Gleichspannung und Wechselspannung.

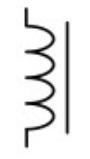4.1 Gleichspannung
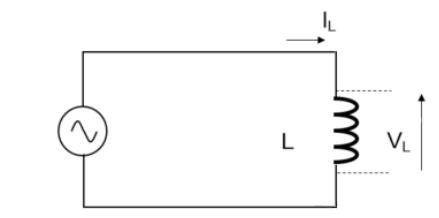
Wie im Schaltplan dargestellt, fließt der Strom zum Induktor, wenn der Schalter geschlossen ist und eine Gleichspannung an den Induktor angelegt wird. Wenn der Strom zum Induktor (Wicklung) fließt, ändert sich auch der erzeugte Magnetstrahl und es entsteht eine elektromotorische Kraft (induzierte elektromotorische Kraft) am Induktor. Im Grunde handelt es sich bei einer Induktivität um eine separate Wicklung, daher wird sie „Selbstinduktivität“ genannt. Diese elektromotorische Kraft wird in der entgegengesetzten Richtung des Stroms erzeugt und verhindert so den Anstieg des Stroms. Im Gegenteil: Sobald der Schalter getrennt wird und der Strom zu sinken beginnt, verhindert die Induktivität, dass der Strom abnimmt.

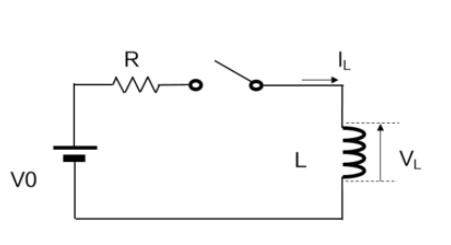
Strom (IL) stellt die folgende Situation dar: Wenn der Schalter geschlossen ist, fließt der Strom ab, aber aufgrund der Behinderung des Anstiegs des elektromotorischen Kraftstroms steigt der Strom mit einer bestimmten Zeitkonstante an. Nach dem Anstieg hängt es von der Widerstandskomponente ab und es fließt ein konstanter Strom durch. Sobald der Schalter geöffnet wird, nimmt der Strom ab, wird aber nach einer bestimmten Zeitkonstante auf die gleiche Weise Null.

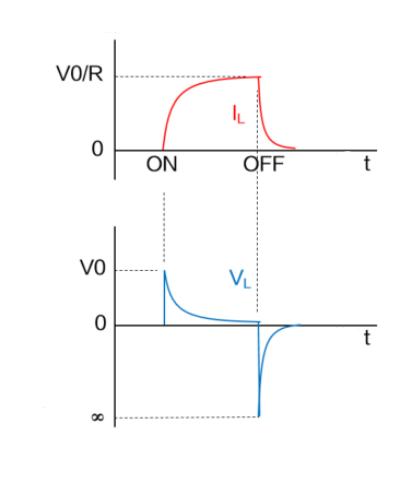
Die Spannung (VL) stellt die elektromotorische Kraft des Induktors dar, wenn der Schalter geschlossen und geöffnet ist. Wie in der Formel gezeigt, ist die Änderungsrate zwischen der am Induktor erzeugten elektromotorischen Kraft und dem Strom （ Δ I/ Δ t) Direkt proportional.

Wie die aktuelle Wellenform zeigt, steigt der Strom bei geschlossenem Schalter langsam an, sodass die elektromotorische Kraft nur auf die Versorgungsspannung ansteigt. Beim Ausschalten des Schalters wird der Strom sofort unterbrochen, was zu einem starken Abfall des Stroms und einem Anstieg der Änderungsrate pro Zeiteinheit im Vergleich zum Einschalten des Schalters führt, was zu einer höheren elektromotorischen Kraft führt.
Darüber hinaus geht der Strom beim Trennen des Schalters nicht sofort auf Null zurück, da aufgrund der von der Induktivität erzeugten Hochspannung ein Entladestrom durch die Anschlüsse des Schalters fließt.
Der Grund dafür, dass eine so hohe elektromotorische Kraft erzeugt werden kann, liegt darin, dass der Induktor, wie am Anfang des „sogenannten Induktors“ erwähnt, in der Lage ist, elektrische Energie in magnetische Energie umzuwandeln und diese im Inneren des Induktors zu speichern. Die akkumulierte Energie kann durch die folgende Gleichung dargestellt werden, die direkt proportional zur Größe des Induktivitätswerts ist.

Wechselspannung
In der obigen Beschreibung wird beschrieben, dass die Größe der am Induktor erzeugten elektromotorischen Kraft direkt proportional zur Änderungsrate des zum Induktor fließenden Stroms ist, was auch bei Wechselstromwellenformen der Fall ist.

(1) Erstens: Wenn der Strom von Null ansteigt, ist die Änderungsrate des Stroms maximal, was zu einem Spannungsanstieg führt. Allerdings verlangsamt sich die Spannung, wenn der Strom ansteigt, und an dem Punkt, an dem der Strom sein Maximum erreicht (die Änderungsrate des Stroms ist Null), wird die Spannung Null.
(2) Wenn der Strom von seinem Maximalwert abzunehmen beginnt, wird eine negative Spannung erzeugt, und wenn der Strom Null erreicht (die Änderungsrate des Stroms ist maximal), ist die Spannung am niedrigsten.
Für die Bereiche (3) und (4) gilt die gleiche Situation.

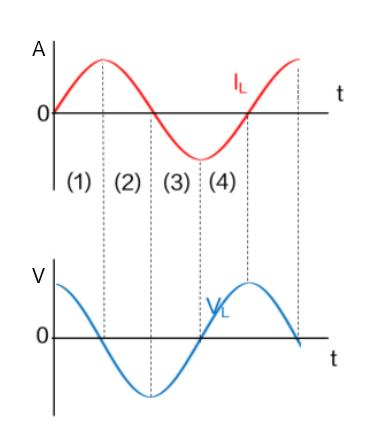
Wenn bei der Betrachtung der Wellenformen von Strom und Spannung die Stromwellenform eine Sinuswelle ist, dann ist auch die Spannungswellenform eine Sinuswelle. Darüber hinaus lässt sich verdeutlichen, dass der Stromverlauf im Vergleich zum Spannungsverlauf um 1/4 Zyklus abweicht (die Phasenverzögerung des Stroms beträgt 90°).
Als Reaktion auf die große Stromänderung entsteht eine größere Spannung, und es kann auch verstanden werden, dass die Spannung bei hohen Frequenzen umso höher ansteigt, je höher die Stromänderungsrate ist.
Die tatsächliche Spannung des Induktors ist jedoch dieselbe wie die Spannung der Wechselstromversorgung. Wenn wir also die Spannung als Referenz betrachten, kann man sagen, dass der durch sie fließende Strom abnimmt, wenn die Frequenz bei konstanter Spannung steigt.
Das heißt, je höher die Frequenz bei der Kommunikation, desto schlechter fließt der Strom durch und die Induktivität wirkt wie ein Widerstand.
Wir nennen dies die Induktivität einer Spule (Ω). Die Impedanz und der durchfließende Strom können durch die folgende Gleichung dargestellt werden.