Analyse von Impedanz, Eingangsimpedanz und Ausgangsimpedanz

Impedanz ist ein Sammelbegriff für Widerstand und Reaktanz, und der größte Unterschied zwischen Widerstand und Reaktanz besteht darin, dass die Widerstandsstrombegrenzung (Ohmsches Gesetz) gleichzeitig elektrische Energie verbraucht. Die Reaktanz ist auf den Strom begrenzt und verbraucht keine elektrische Energie (ohne Arbeit zu leisten). Der Widerstand hat sowohl bei Gleichstrom als auch bei Wechselstrom eine begrenzte Stromwirkung, während die Reaktanz in Wechselstromumgebungen nur eine begrenzte Stromwirkung hat.

Die Eingangsimpedanz bezieht sich auf die äquivalente Impedanz am Eingangsende eines Stromkreises. Fügen Sie dem Eingangsanschluss eine Spannungsquelle U hinzu und messen Sie den Strom I am Eingangsanschluss. Dann beträgt die Eingangsimpedanz Rin U/I. Sie können sich das Eingangsende als die beiden Enden eines Widerstands vorstellen, und der Widerstandswert dieses Widerstands ist die Eingangsimpedanz.

Wenn bei gleicher Eingangsspannung die Eingangsimpedanz sehr niedrig ist, muss ein großer Strom fließen, was die Stromausgangsfähigkeit der vorherigen Stufe testet; Wenn die Eingangsimpedanz hoch ist, ist nur eine geringe Strommenge erforderlich, was die Stromausgangsfähigkeit der Frontstufe erheblich belastet. Versuchen Sie daher beim Schaltungsdesign, die Eingangsimpedanz so weit wie möglich zu erhöhen.

Die Eingangsimpedanz unterscheidet sich nicht von einer gewöhnlichen Reaktanzkomponente, da sie die Größe der Stromblockierungswirkung widerspiegelt.

Bei spannungsgesteuerten Schaltkreisen gilt: Je größer die Eingangsimpedanz, desto geringer ist die Belastung der Spannungsquelle, was die Ansteuerung erleichtert, ohne die Signalquelle zu beeinträchtigen. Bei stromgesteuerten Schaltkreisen ist die Belastung der Stromquelle umso geringer, je kleiner die Eingangsimpedanz ist.

Daher können wir davon ausgehen, dass bei Verwendung einer Spannungsquelle zum Antrieb gilt: Je größer die Eingangsimpedanz, desto besser. Wenn es von einer Stromquelle angetrieben wird, ist es umso besser, je kleiner die Impedanz ist (Hinweis: Nur für Niederfrequenzschaltungen geeignet, bei Hochfrequenzschaltungen sollte auch eine Impedanzanpassung berücksichtigt werden.) Darüber hinaus muss bei der Erzielung der maximalen Ausgangsleistung die Impedanz berücksichtigt werden Die Anpassung sollte ebenfalls berücksichtigt werden.Ausgangsimpedanz

Die Ausgangsimpedanz umfasst die interne Impedanz der äquivalenten Spannungsquelle (Thevenin-Ersatzschaltung) oder der äquivalenten Stromquelle (Norton-Ersatzschaltung) des unabhängigen Stromnetz-Ausgangsports. Sein Wert entspricht der vom Ausgangsanschluss aus gesehenen Eingangsimpedanz, wenn die unabhängige Stromversorgung auf Null eingestellt ist.

Unabhängig von der Signalquelle, dem Verstärker und der Stromversorgung besteht ein Problem mit der Ausgangsimpedanz. Die Ausgangsimpedanz ist der Innenwiderstand einer Signalquelle. Ursprünglich sollte für eine ideale Spannungsquelle (einschließlich Netzteil) der Innenwiderstand 0 sein, bzw. die Impedanz einer idealen Stromquelle sollte unendlich sein. Der Ausgangsimpedanz bedarf beim Schaltungsdesign besondere Aufmerksamkeit.

In der Realität können Spannungsquellen dies nicht erreichen, und eine ideale Spannungsquelle wird oft in Reihe mit einem Widerstand r geschaltet, um einer tatsächlichen Spannungsquelle zu entsprechen. Der Widerstand r in Reihe mit der idealen Spannungsquelle ist der Innenwiderstand der Signalquelle/des Verstärkerausgangs/der Stromversorgung.

Wenn diese Spannungsquelle die Last mit Strom versorgt, fließt ein Strom I durch die Last und erzeugt I an diesem Widerstand × Der Spannungsabfall von r. Dies führt zu einer Verringerung der Ausgangsspannung des Netzteils und begrenzt dadurch die maximale Ausgangsleistung.

Ebenso sollte eine ideale Stromquelle eine Ausgangsimpedanz von unendlich haben, tatsächliche Schaltungen sind jedoch nicht möglich.

Die Ausgangsimpedanz bezieht sich auf die äquivalente Impedanz der Schaltung, wenn die Schaltungslast vom Ausgangsanschluss der Schaltung in entgegengesetzter Richtung betrachtet wird. Tatsächlich bezieht es sich hauptsächlich auf die von der Energiequelle am Ausgangsende gemessene Impedanz, die allgemein als Innenwiderstand bekannt ist.

Impedanzdenkende Analyse von Schaltkreisen

Wie in der folgenden Abbildung dargestellt, liefert V1 weiterhin Strom an R1, und der Stromkreis in der Abbildung wird durch den grünen Pfeil dargestellt. Welche Methoden haben wir, wenn wir den Stromfluss zu R1 steuern wollen?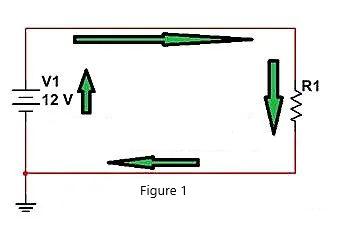

Die gebräuchlichste Methode besteht darin, die Verbindung zwischen V1 und R1 zu trennen und den Stromkreis zu unterbrechen. Wie in der folgenden Abbildung dargestellt.

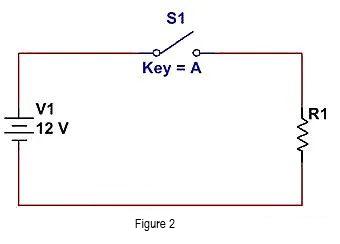
Alternativ können wir R1 umgehen, wie in der folgenden Abbildung gezeigt. Fügen Sie vor R1 einen Draht hinzu, um den Strom auf den Pfad mit niedriger Impedanz zu leiten, und R1 erhält einen vernachlässigbaren Strom.

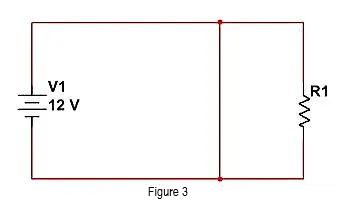
Die beiden oben genannten Methoden sind sehr einfach: Sie trennen entweder den Pfad von V1 zu R1 vollständig oder schließen R1 kurz, wodurch das Problem vollständig gelöst wird. Aber in der Welt des Ingenieurwesens können wir es nicht so sauber und ordentlich machen und legen oft Wert auf ein „ähnliches“ Prinzip. Ansatz. Im „Kurzschlussmodell“ können wir also nur eine „niedrige Impedanz“ erreichen, während wir im „Leerlaufmodell“ nur eine „hohe Impedanz“ erreichen können. Wenn die Energie erheblich „gedämpft“ wird, gehen wir davon aus, dass sie dem Standard entspricht.

Wie in der folgenden Abbildung dargestellt, ist das tatsächliche Leistungslastmodell dargestellt. Sehen wir uns an, wie man durch Anpassen der Impedanz einen Schalteffekt erzielt. In tatsächlichen Stromkreisen unterliegen Stromquellen Einschränkungen hinsichtlich der Ausgangskapazität und des Innenwiderstands. Je größer der Ausgangsstrom, desto niedriger die Ausgangsspannung.

Die folgende Schaltung hat einen Innenwiderstand von 0,1 Ω und eine Last von 1K Ω. In der aktuellen Situation setzt sich die an beiden Enden der Last erhaltene Spannung aus dem Innenwiderstand und der R2-Teilspannung zusammen. Wir können V=5V * (1K/(1K+0,1))=4,9999V, I=5V/1000,1 Ω=4,9mA berechnen.

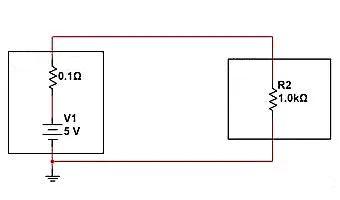
Wenn wir das „Open-Circuit-Modell“ verwenden, Methode zum Unterbrechen des Stromkreises. Wie sollten wir die Impedanz anpassen? Es besteht darin, einen Widerstand, der viel größer als 1 K ist, in Reihe zwischen die Stromversorgung und die Last zu schalten und eine Reihenspannungsteilung durchzuführen, um die an R2 erhaltene Spannung zu reduzieren. Wie in der folgenden Abbildung dargestellt, wird ein 1M-Widerstand in Reihe mit dem Lastspannungsteiler geschaltet. Wir können die endgültige Spannungsverteilung zwischen den beiden Enden der Last berechnen:

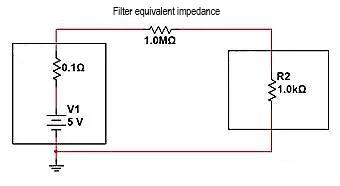
V=5V * (1K/(0,1+1000K+1K))=0,00499V, I=5V/1001000,1 Ω=0,0049mA. Die Amplitude wurde um fast das 1000-fache abgeschwächt, und im technischen Denken ist R2 nahezu „unverbunden“.

Wenn wir das „Kurzschlussmodell“ verwenden, Methode zum Trennen von R2, wie sollten wir sie anpassen? Dazu wird ein Widerstand, der viel kleiner als 0,1 Ω ist, am vorderen Ende der Last parallel geschaltet und die Spannung in Reihe mit dem internen Widerstand geteilt, was zu einer kleineren Spannung an R2 führt.

Wie in der folgenden Abbildung dargestellt, entspricht die Filtermaßnahme einem parallelen 0,005-Ω-Widerstand und einem internen Widerstandsspannungsteiler. Wir können die endgültige verteilte Spannung zwischen den beiden Enden der Last R2 berechnen:

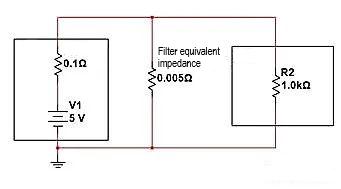
V = 5 V * (0,0049/(0,1 + 0,0049) = 0,233 V. Die Amplitude wurde um fast das Zwanzigfache abgeschwächt, und im technischen Denken ist R2 auch so, als ob man „nicht verbunden“ wäre.

Das Obige ist das theoretische Modell von Halbleiterschaltkreisen am Beispiel von Wechselrichterschaltungen:

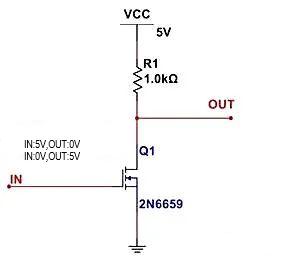
Wenn das IN-Ende eingeschaltet ist, sagen wir, dass der MOS-Transistor Q1 leitet. An diesem Punkt ist der Leitungszustand gleichbedeutend damit, dass Q1 zu einem Widerstand mit einer Impedanz von mehreren zehn Milliohm wird und dann die Spannung mit dem Widerstand R1 geteilt wird. Wenn der Pull-up-Widerstand R1 zu klein ist und auch mehrere zehn Milliohm beträgt, kann der OUT-Anschluss keinen niedrigen Pegel ausgeben, selbst wenn IN hoch ist und Q1 leitet.

Wenn das IN-Ende ausgeschaltet ist, sagen wir, dass der MOS-Transistor Q1 abgeschaltet ist. An diesem Punkt ist der Abschaltzustand gleichbedeutend damit, dass Q1 zu einem Widerstand mit einer Impedanz von einigen Megaohm wird und die Spannung mit dem Widerstand R1 geteilt wird. Wenn der Pull-up-Widerstand R1 zu groß ist, was ebenfalls einige Megaohm beträgt, kann der OUT-Anschluss keinen hohen Pegel ausgeben, selbst wenn IN niedrig ist und Q1 abgeschaltet ist.

Um Schaltkreise tiefgreifend zu verstehen, ist es daher notwendig, sie mit Impedanzdenken zu analysieren.

Filterschaltung zur Impedanz-Denkanalyse

Analysieren Sie hier die Filterschaltung mithilfe des Impedanzdenkens.

In praktischen technischen Anwendungen enthält ein Leistungsausgang oft Wechselstromkomponenten unterschiedlicher Frequenz, sowohl was wir wollen als auch was wir nicht wollen. Die Impedanz von Induktivität und Kapazität variiert mit der Frequenz. Genau aufgrund dieser Eigenschaft sind Induktivitäten und Kondensatoren zu den Hauptakteuren in Filterschaltungen geworden.

Die folgende Schaltung wird immer noch verwendet, vorausgesetzt, dass die Stromversorgung eine Spektralkomponente von
enthält 0–1 GHz.

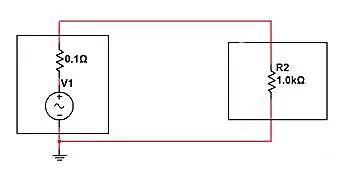
Wenn wir hochfrequente Wechselstromkomponenten für Last R2 herausfiltern wollen, werden wir feststellen, dass sowohl die Serieninduktivität als auch die Parallelkapazität die Anforderungen erfüllen können.
Wie in der folgenden Abbildung dargestellt: Wie stark wird die 100-MHz-Wechselstromkomponente abfallen, wenn eine 16uH-Induktivität in Reihe zwischen der Stromversorgung und der Last geschaltet wird? Gemäß der Impedanzformel der Induktivität: ZL=2 π fL=2 * 3,14 * 100MHz * 16uH, kann ZL=10K erhalten werden.

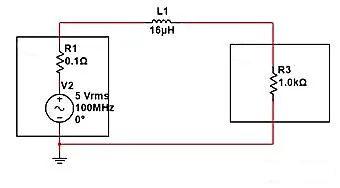
Gemäß der Reihenspannungsteilerformel ist die Spannung/Eingang an beiden Enden von R3=R3/(R3+ZL)=1K/11K=0,0909. Wenn also die Amplitude der Stromversorgung 5 V beträgt, beträgt die Amplitude an beiden Enden von R3 nur 5 V * 0,0909 = 0,45 V.

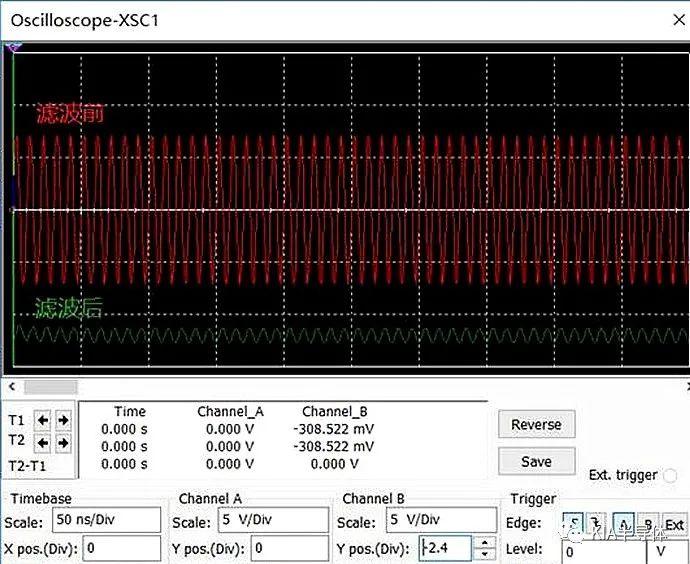
Verwenden Sie bei 100 MHz ein Oszilloskop, um die Wellenform vor und nach der Filterung zu messen. Der Vergleich zeigt, dass die 100-MHz-Wellenform einen Effekt hat und der tatsächliche Messwert 0,449 V beträgt, was mit den Analyseergebnissen übereinstimmt.

Impedanzdenkende Analyse von Tiefpassfiltern

Durch die Reihenschaltung einer Induktivität zwischen der Stromversorgung und der Last und die Parallelschaltung eines Kondensators am vorderen Ende der Last wird eine Tiefpassfilterschaltung gebildet.

Wie folgt: Wenn C1=1uF und L1=22uH, wie groß ist der Dämpfungsgrad der Filterschaltung zum
? 100-MHz-Wechselstromkomponente?

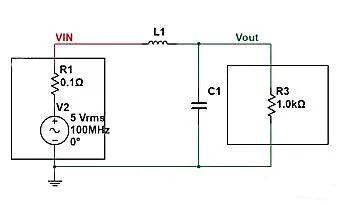
An diesem Punkt wird die Schaltung parallel mit der Impedanz Zc des Kondensators (C1) und R3 geschaltet und dann mit der Impedanz ZL der Induktivität (L1) geteilt. Wir können also die Impedanzgleichung auflisten (die eine einfache Reihenspannungsteilerformel ist).

Dämpfungsamplitude = Vout/Vin = (Zc//R3)/(ZL+(Zc/R3)

Darunter Zc=1/2 π fC und ZL=2 π fL. Bei R3=1K Ω kann daraus geschlossen werden, dass Zc=0,0015 Ω, Zc/R=0,00149 Ω.

ZL=13816 Ω, die Dämpfungsamplitude kann als 0,00149/(13816,00149)=0,000000178 erhalten werden.

Es ist ersichtlich, dass die 100-MHz-Wechselstromkomponente die Tiefpassfilterschaltung von 22 uH und 1 uF kaum passieren kann. Gleichzeitig sehen wir auch, dass die Belastung R3 die Filterwirkung des Filters beeinflussen kann. Daher stellen wir manchmal fest, dass dieselbe Filterschaltung auf dieser Schaltung gut funktioniert, auf anderen Schaltungen jedoch schlecht.